Stack Filters

Many applications of signal processing deal with processing an input signal and producing an output signal. A common scenario occurs when a signal is transmitted through a channel that distorts it with noise. Consequently, the receiver must attempt to reconstruct the original signal as closely as possible from the distorted one. In general, this is a difficult problem, especially if the receiver has no knowledge of the signal or noise characteristics. However, in many practical situations, the statistics of the noise are known. For instance, if it is known that the noise is modeled by an additive Gaussian process, then a linear filter is known to be optimal under the mean square error criterion. This optimality result is one of the primary reasons that linear filters have been a primary tool throughout the history of signal processing. Other reasons for this are that linear filters are well understood and they have some elegant theoretical properties. For example, linear filters that minimize the mean square error can usually be found in closed form. Their simplicity follows mainly from the linearity or superposition property. Furthermore, linear filters offer acceptable performance in many situations.

In many instances, however, it is impossible to find an acceptable linear filter,  when noise is non-additive or non-Gaussian. For example, it is well known that linear filters can remove additive high frequency noise as long as the signal and the noise do not overlap in the frequency domain. However, in two-dimensional signal processing (e.g., image processing), the signal often contains meaningful high frequency components, such as edges and fine image details. A linear low-pass filter, if applied to such a signal, would blur sharp edges,  producing unacceptable results, necessitating the use of nonlinear filters.

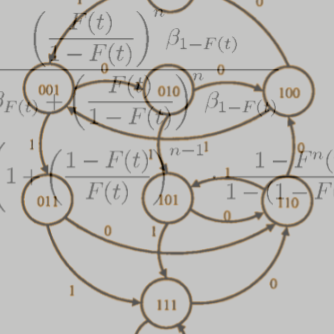
Our work in nonlinear filters centered on the class of so-called stack filters, which are sliding window operators based on monotone Boolean functions.  Included in this class of filters are the well-known median filter, rank-order filters, order-statistics based filters, and morphological filters with flat structuring elements.  We developed analysis approaches that use dynamical systems theory (finite automata and Markov chains) to determine the statistical properties of stack filters, such as their output distributions and robustness characteristics [1-5].  We also developed optimization methods for stack filters for best detail preservation, while optimally removing noise [7,8] and proved that the class of stack filters is highly robust to outliers [9].

We showed that using the theory of regular languages, one can analyze the filter’s long-run behavior.  For example, so-called root signals are signals that are preserved by the filter [6]. This idea is equivalent to attractors in dynamical systems [10].

Publications

1. I. Shmulevich, O. Yli-Harja, K. Egiazarian, J. Astola, “Output Distributions of Recursive Stack Filters,” IEEE Signal Processing Letters, vol. 6, no. 7, pp. 175-178, July, 1999.
2. P. Koivisto, O. Yli-Harja, A. Niemistö, and I. Shmulevich, “Breakdown Probabilities of Recursive Stack Filters,” Signal Processing, Vol. 81, No. 1, pp. 227-231, December 2000.
3. O. Yli-Harja, I. Shmulevich, J. A. Bangham, R. Harvey, S. Dasmahapatra, S. Cox, “Run-length Distributions of Recursive Median Filters Using Probabilistic Automata,” Proceedings of Scandinavian Conference on Image Analysis, Kangerlussuaq, Greenland, June 7-11, 1999.
4. I. Shmulevich, J. L. Paredes, G. R. Arce, “Output Distributions of Stack Filters Based on Mirrored Threshold Decomposition,” IEEE Transactions on Signal Processing, Vol. 49, No. 7, pp. 1454-1460, July 2001. (published correction due to errors in production is here…)
5. I. Shmulevich, K. Egiazarian, O. Yli-Harja, and J. Astola, “Output Distributions of Stack Filters Using Ordered Binary Decision Diagrams,” Journal of Signal Processing, vol. 4, no. 2, pp. 195-200, March 2000,
6. I. Shmulevich, O. Yli-Harja, K. Egiazarian, J. Astola, “Root signals of stack filters and regular languages,” Conference on Computer Science and Information Technologies, Yerevan, Armenia, August 17-23, 1999.
7. I. Shmulevich, V. Melnik, K. Egiazarian, “Optimization of Stack Filters Using Sample Selection Probabilities,” Proceedings of IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, Antalya, Turkey, June 20-23, 1999.
8. I. Shmulevich, V. Melnik, K. Egiazarian, “The Use of Sample Selection Probabilities for Stack Filter Design,” IEEE Signal Processing Letters, vol. 7, no. 7, pp. 189-192, July 2000.
9. I. Shmulevich, O. Yli-Harja, J. Astola, A. Korshunov, “On the Robustness of the Class of Stack Filters,” IEEE Transactions on Signal Processing, Vol. 50, No. 7, pp. 1640-1649, July 2002.
10. M. Nykter, J. Kesseli, and I. Shmulevich, “Dynamical systems analysis of stack filters,” in I. Tabus, K. Egiazarian, and M. Gabbouj, editors, Festschrift in honor of Jaakko Astola on the occasion of his 60th Birthday, pp. 169-181, Tampere International Center of Signal Processing, 2009.
11. I. Shmulevich and G. R. Arce, “Spectral design of weighted median filters admitting negative weights,” IEEE Signal Processing Letters, Vol. 8, No. 12, pp. 313-316, 2001.